Copyright Notice:  Copyright (C) Newman K. Lin, Ph.D., PE., The Lin Institute, All rights reserved. If you want to use the information of this document, Please contact Dr. Lin by e-mail: Lin_Institute@yahoo.com
Case Study:  On superior penile size and growth for sexual orgasm and the limitation of the erectile angle with penile size - the cantilevel beam theory and the deflection induced tissues scarring
Reader: 9/03/2010> 
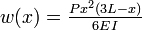
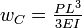
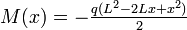
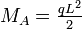
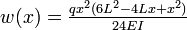
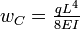
As a fellow scientist, I hypothesize that the maximum size a man can balloon to and still have a rock hard 12 - 2 o'clock erection is under between 6.75-9.50 inches in length and 6-7.50 inches in girth, which includes the glans circumference as well.  For example, at maximum ballooning stage, a man can reach 8.5 inches in length, 6.50 inches girth midshaft and 6.75 inches around in the glans or head.  Thus, I would add these variables:

8.5 + 6.50 + 6.75 =  21.75

>From my calculations, it is nearly impossible for a man to have at least a 2 o'clock erection or higher angle with an index OF 22.00 OR GREATER. THE INDEX MUST BE BELOW 22.00. SO THE EXAMPLE SHOWN HERE IS VERY CLOSE TO THE MAXIMUM SIZE OF LENGTH, MIDSHAFT GIRTH AND HEAD SIZE A MAN CAN ATTAIN AND STILL HAVE A 2 O'CLOCK OR HIGHER ANGLE ERECTION. OF COURSE, THERE ARE OTHER PERMUTATIONS TO ACHIEVE THIS INDEX, BUT THEY MUST FOLLOW THE LENGTH AND GIRTH LIMITATIONS POSED ABOVE. 

I PROPOSE THAT THE MAXIMUM DIMENSIONS TO ACHIEVE THIS 2 O'CLOCK OR HIGHER ANGLE ERECTION ARE AS FOLLOWS:

LENGTH: NO MORE THAN 9.5 INCHES IN LENGTH

GIRTH: MIDSHAFT AND HEAD SIZE NO MORE THAN 7.5 INCHES IN CIRCUMFERENCE.



HERE ARE THE POSSIBLE COMBINATIONS: Note that head size is either equal or slightly larger than the shaft to accentuate the drumstick effect you refer to.  All the following numbers are in inches.

Length  midshaft    glans     INDEX TOTAL
6.75 +    7.50 +     7.50   =   21.75,
7.00 +    7.25 +     7.50   =   21.75,
7.25 +    7.25 +     7.25   =   21.75,
7.50 +    7.00 +     7.25   =   21.75,
7.75 +    7.00 +     7.00   =   21.75,
8.00 +    6.75 +     7.00   =   21.75,
8.25 +    6.75 +     6.75   =   21.75,
8.50 +    6.50 +     6.75   =   21.75,
8.75 +    6.50 +     6.50   =   21.75,
9.00 +    6.25 +     6.50   =   21.75,
9.25 +    6.25 +     6.25   =   21.75,
9.50 +    6.00 +     6.25   =   21.75

I WOULD APPRECIATE YOUR EXPERTISE AND VALUABLE INSIGHT REGARDING MY HYPOTHESIS AND RESEARCH.  THANKS YOU FOR YOUR ATTENTION AND TIRELESS SUPPORT DR. LIN.  PLEASE NOTE THAT WE ARE DISCUSSING THE MAXIMUM CAPACITY OF YOUR BALLOONING METHOD BECAUSE I KNOW THAT YOU BELIEVE THAT A 12 - 2 O'CLOCK 6-7 INCH LENGTH ERECTION IS SUFFICIENT FOR MOST WOMEN.  THESE EXTREME SIZES ARE FOR THE WOMEN THAT CAN ACCOMODATE SUCH A STRONG YANG IMPLEMENT.
Dr. Lin: 9/04/2010>
I don't know how you came up with this Index Total of 21.75.
You may be right since I have never seen any penis with 9.50 inches long can erect to the 2 o'clock position, the free-constraint, natural erectile angle of the initial (first-stage) erection which can be ballooned to the 1  o'clock position (the 2nd stage erection).
We can use the engineering  Cantilever principle and its bending moment to analyze the deflection of an erecting penis
A penis of 9.5 inches long and 6.0 inches circumference weighs about 600 grams x 980 cm/sec/sec  and its distribution load is about q = 24561.4 grams/sec/sec
The deflection  depends  E ,  the elastic modulus of tunica albuginea   and that I , the second moment of area = π r4 / 4 where r is radius (I = 416.7 cm4)
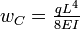The deflection at the end of the glans  w_C = \tfrac{qL^4}{8EI} , where L= 9.5 x 2.52 cm = 23.94 cm
Wc =  2420116.178/E  cm
Unless the elastic modulus of tunica albuginea is like a steel, the penile shaft should have big deflection by gravity.  It is possible to have very stiff elastic modulus to aim at the 1 o'clock position which is anti-gravity.  The penile shape is slight curved up to the 1 o'clock position while the tangential direction of the penile shaft at the penile suspension ligament or pubis points to the 2 o'clock position.  The penile upward curvature develops in the 2nd stage erection which stretches and expands the corpus spongiosum, with a pair of powerful bulb-cavernous arteries, more than the two corpus cavernosums which have one cavernous artery in the center of each cyclinder. However, if your penis can not aim high, you have have a gravitational deflection, particularly, for a huge penis. Chronic big deflection will scar the tunica albuginea. In particular, the huge penis will be bended and forced down by the underwear.  under the bending stress and strain, collagen scar tissues develop over the superior side of the shaft or near or at the penile  suspension ligament (or the ligaments themselves) to prohibit the huge penis to aim high.
I have also found that there is no much difference in size for the  huge penis in the flaccid and erecting state. That is, the huge penile erectile size is almost the same as the flaccid one. This means, the penile arteries won't dilate much in the erectile state, or they have been actually pre-dilated in the flaccid state. Thus, the penile arteries for the huge penis  are like the arteries in the other parts of the body, and always dilate for the blood flow to come in, becoming the major branches of the entire blood circulation. This allows the penis to grow with the other parts of the body since it takes nutrients and hormones day and night with constantly dilating the arteries. Also, men with a huge penis have a very high testosterone and DHT level to stimulate the penile tissues to grow 24 hours a day during their puberty. 
In the regular penis, the blood flows into the penis only when the arteries are dilating during sexual arousal, erection and sleeping. This limits the penile growth  during puberty.  Teenage boys have a very frequent erection, maybe about 12 hours a day at least,  during the penile growth period. The longer the erection time (30-60 minutes each time), the higher the erection frequency (several times a day every day), and the higher the hGH, DHEA, testosterone and DHT in the bloodstream, the faster and bigger the penis grows.  This is why the penile ballooning enlargement method requires at least 30 minutes erection so that the hGH, DHEA, testosterone, DHT, oxytocin, and beta-endorphin can help sufficient time to activate the Transformation Growth Factor beta-3 and  Cytokeratin 16 genes.
My another discovery is that the huge penis usually looks soft  and no life since there is not erecting at all even during sexual arousal. The normal 2nd-stage erecting penis becomes very rigid and hot, like a heating rod,  and can not be bended over or down.

Here are references for the application of the cantilevel beam theory to the deflection of a huge penis.

http://en.wikipedia.org/wiki/Cantilever
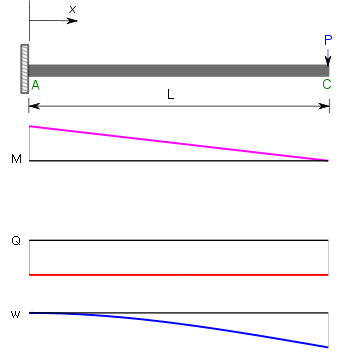
http://en.wikipedia.org/wiki/File:CantBeamPointLoad.svg
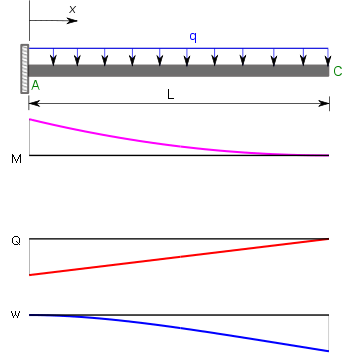
http://en.wikipedia.org/wiki/Beam_theory

Cantilever beams

Another important class of problems involves cantilever beams. The bending moments (M) , shear forces (Q), and deflections (w) for a cantilever beam subjected to a point load at the free end and a uniformly distributed load are given in the table below[5].

Distribution Max. value
Cantilever beam with end load CantBeamPointLoad.svg
M(x) = P(x − L) MA = PL
Q(x) = P Qmax = P
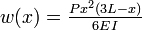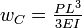w(x) = \tfrac{Px^2(3L-x)}{6EI} w_C = \tfrac{PL^3}{3EI}
Cantilever beam with uniformly distributed load CantBeamDistLoad.svg
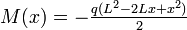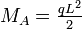M(x) =-\tfrac{q(L^2-2Lx+x^2)}{2} M_A = \tfrac{qL^2}{2}
Q(x) = q(L − x), QA = qL
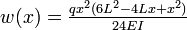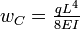w(x) = \tfrac{qx^2(6L^2-4Lx+x^2)}{24EI} w_C = \tfrac{qL^4}{8EI}